Thinking Mathematically: Chapter 5 Solutions
Bee Genealogy
[!info] Bee Genealogy Male bees hatch from unfertilized eggs and so have a mother but no father. Female bees hatch from fertilized eggs. How many ancestors does a male bee have in the twelfth generation back? How many of these are males?
Entry
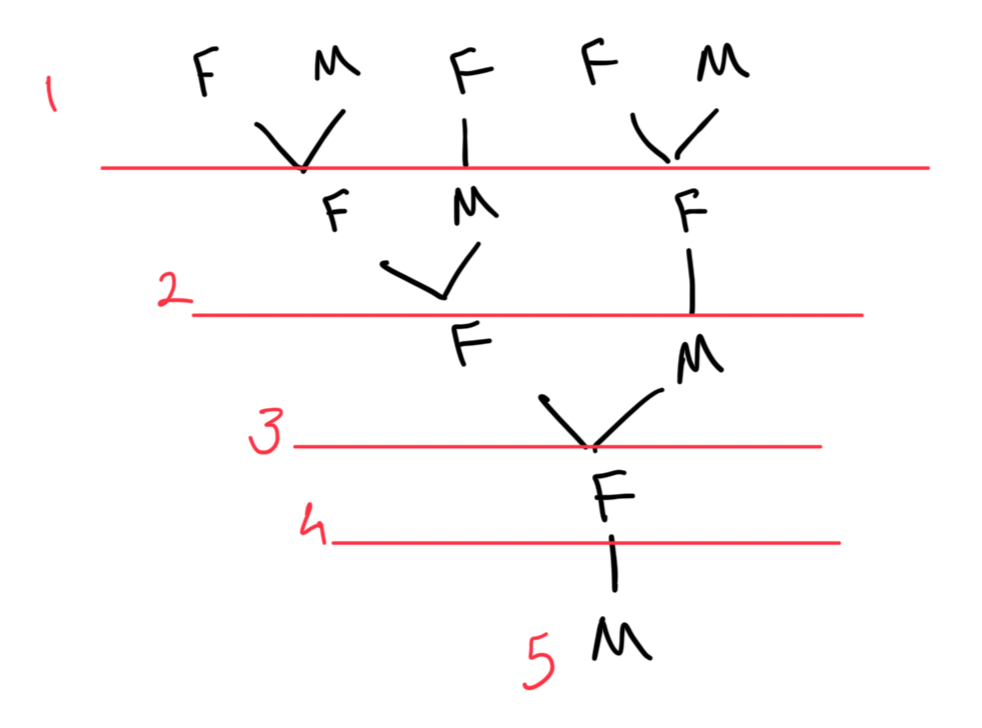
We’ll specialise by drawing a sample diagram. The red numbers indicate the ancestors.
Attack
Looking at the diagram, a clear pattern emerges $1, 1, 2, , 3, 5, …$ . This is the Fibonacci sequence.
Conjecture: The total number of ancestors in any generation n is the nth Fibonacci number.
We now try to understand how the number of ancestors in any generation n relates to previous generations.
- The total ancestors in generation $n$ which we call $A_n$ are the parents of the ancestors in generation $n-1$.
- The ancestors in generation $n-1$ are made up of $M_{n-1}$ males and $F_{n-1}$ females.
- Each of those $F_{n-1}$ females has two parents in generation $n$.
- Each of those $M_{n-1}$ males has one parent in generation $n$.
From this, we can build a structural argument:
- The number of females in generation $n$, $F_n$, is the sum of the mothers of the previous generation’s males and females. That’s one mother for each, so $F_n = M_{n-1} + F_{n-1}$, which is simply the total number of ancestors in the previous generation $A_{n-1}$.
- The number of males in generation $n$, $M_n$, comes only from the female ancestors in generation $n-1$. So, $M_n = F_{n-1}$.
- The total number of ancestors in generation $n$ is $A_n = F_n + M_n$.
- Substituting our findings, we get: $A_n = A_{n-1} + F{n-1}$.
- And since $F_{n-1} = A_{n-2}$ (the number of females in one generation equals the total ancestors of the generation before it), we arrive at the final structural link: $A_n = A_{n-1} + A_{n-2}$.
This formula is the definition of the Fibonacci sequence.
Review
The distinction between a proof and a mathematical structure feels blurry. The AHA moment was seeing the Fibonacci pattern emerge in the total number of ancestors.
Square Dissection
[!info] Square Dissection A number N is called nice if a square can be dissected into N non-overlapping squares. What numbers are nice?
Entry
The key is to use the process of specializing to get a feel for the problem.
What do I KNOW? I’m cutting a large square into smaller, non-overlapping squares. An important clarification, as the book points out, is to check for
hidden assumptions. The problem does not say the smaller squares must be the same size. This is a crucial piece of freedom! * What do I WANT? I want to find the complete set of numbers, N, that are “nice”. I want to characterize them.
What can I INTRODUCE? Diagrams.
Specializing with small numbers:
- N=1: A square is already 1 square. So, 1 is nice.
- N=2, 3: After a few sketches, it seems impossible to dissect a square into 2 or 3 smaller squares. Let’s conjecture that 2 and 3 are not nice.
- N=4: Easy! A simple 2x2 grid of identical squares works. So, 4 is nice.
- N=5: This seems impossible, much like 2 and 3. Let’s conjecture that 5 is not nice.
So far, our set of nice numbers is {1, 4, …} and our “not nice” set is {2, 3, 5, …}.
Attack
The Key Insight: The “+3 Operation”
Take any single square in the K-dissection and dissect it into a 2x2 grid of four smaller squares.
This action removes one square and adds four new ones, for a net gain of three squares. So, if a number K is nice, then K+3 must also be nice.
We know 1 is nice, so applying the +3 operation gives us $1+3=4, 4+3=7, 7+3=10, …$ these are numbers in the form $3k + 1$.
Below we see how we can get 6 and 8.
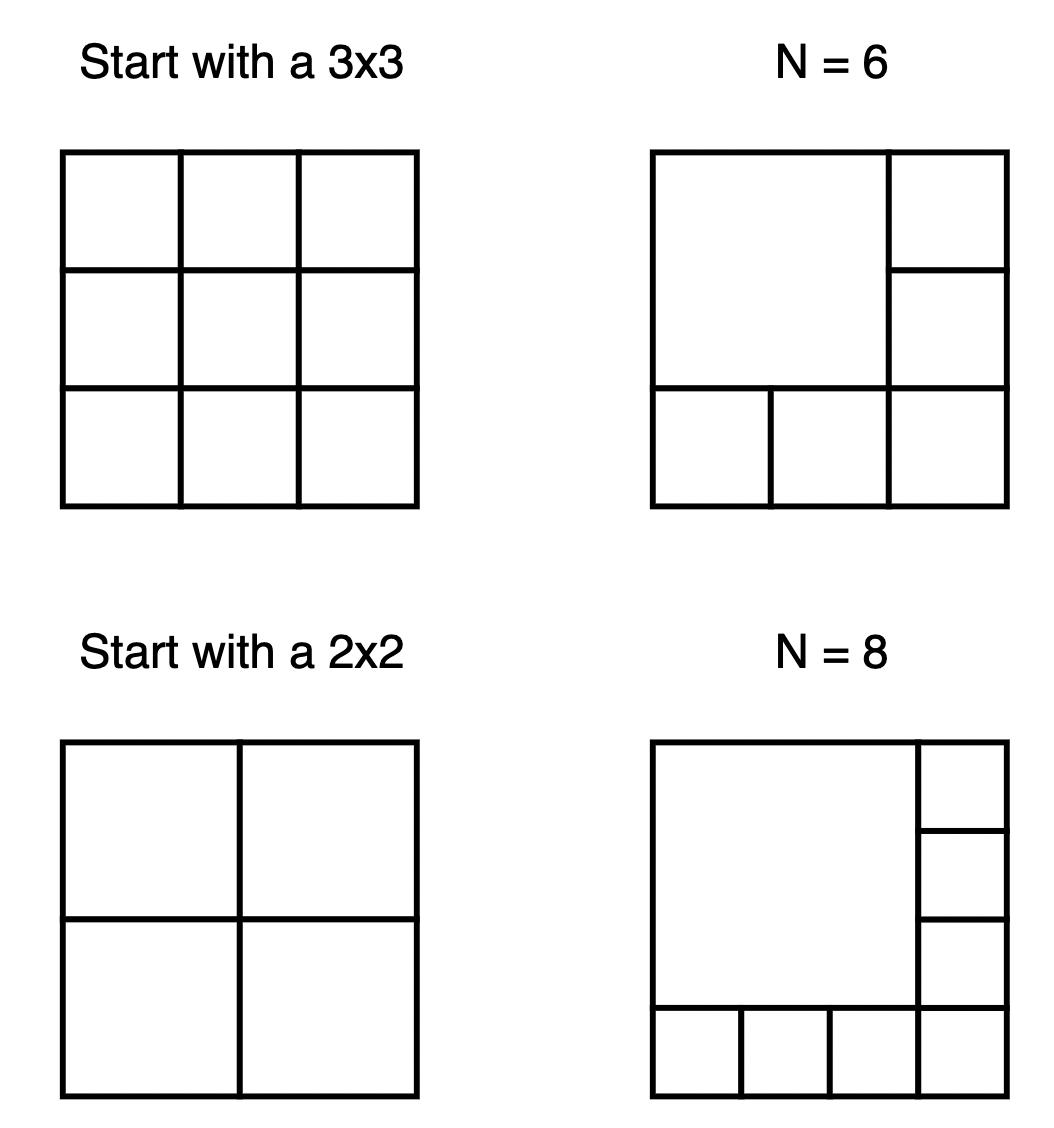
So, we can form a conjecture.
- From 6, we can generate $9, 12, 15, …$ (all numbers in the form $3k$)
- From 7, we can generate $10, 13, 16, …$ (all numbers in the form $3k+1$)
- From 8, we can generate $11, 14, 17, …$ (all numbers in the from $3k+2$)
These three families, taken together, generate every single integer greater than or equal to 6! Why? Because any integer, when divided by 3, must have a remainder of 0, 1, or 2
Review
REFLECT: The key moments were:
- Realizing the squares could be different sizes (avoiding a hidden assumption).
- Discovering the recursive K -> K+3 construction. This turned the problem from a series of special cases into a structured system.
- Realizing we needed more than one base case and searching for them.
- Using a number theory argument (remainders mod 3) to justify that our constructions covered all possibilities.